Perspectives on Conway’s Game of Life

Science has brought the world strong economies and increased quality of life. Though, my personal favorite element to emerge from the pursuit of knowledge is perspective. A change in perspective is evident anywhere where new knowledge is obtained. It also reveals itself in a cellular automaton called Conway’s Game of Life which was created by mathematician John Horton Conway.

All you have to do is google Conway's Game of Life on a desktop browser to see a bunch of pixels emerge and spread across your screen in various patterns. Do not be alarmed. This is not a virus making its way to consume your search results. What you are seeing is a simulation of Conway's Game of Life.

The purpose of this cellular automaton is to demonstrate how complexity can arise from simplicity in evolving systems. In this case there are only four rules:

• Any live cell with fewer than two live neighbors dies.

• Any live cell with two or three live neighbors lives.

• Any live cell with more than three live neighbors dies.

• Any dead cell with exactly three live neighbors becomes a live cell.

These rules in the universe of the automaton can be analogous to the laws of physics of our universe. Much like what can occur in our own chaotic universe, there’s a variety of stable configurations that can occur in the game of life such as this “glider” which can keep its form while also moving through space.

Perhaps this can be analogous to an atom. It’s a very simple yet versatile structure especially when you throw into the mix this “glider gun” which is another stable structure which can produce them continuously.

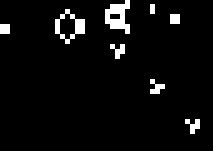
There also exists even more complex configurations which are able to produce glider guns continuously. Several stable configurations exist that have been identified and used as components for more complex structures. The following video demonstrates the full scale to which these four rules can bring about highly complex structures on a 2-dimensional grid.

According to string theory, it may be possible that our four dimensional universe (three dimensions of space and one dimension of time) is floating in a higher dimensional space. Sense we are only capable of perceiving three spatial dimensions it would be impossible for us to observe these higher dimensions. Conway's Game of Life abides by the rules in our universe much like how our universe adheres to a higher set of rules. These two dimensional configurations in the game are only stable for as long as the computer is on and working in our three dimensional universe.

Each time one of these games is started up can be thought of as its own big bang. Of course each different game of life is going to have a different outcome which can be thought of as different universes with the same physics. There are also cellular automaton that have different rules than the game of life which can be thought of as different universes with different laws of physics entirely. If we look at these cells as minuscule areas in two dimensional space then we can think of each area as a Planck length which is the smallest possible measurement in our universe; allowing us to visualize the movement of things in our universe similarly as to how we view this binary set of rules detonating where and how something moves.

Of course, there is some quantum mechanical caveats to this idea if we want to think of the cells on a particle-like scale. For instance, particles behave probabilistically which is to say that they arbitrarily break the rules we understand. Particles are capable of things such as: popping in and out of existence and sometimes tunneling through barriers that would not be expected. Sometimes they are described as being in one location or another. Other times they are described as being in both locations at once. For this reason subatomic particles can only be described through probability theory. Conway's game behaves deterministically so it always adheres to its own set rules. Theoretically, if we could program a cellular automation to behave more randomly we might expect it to be completely chaotic with no lasting configurations. Though, imagine we started such a game and then let it sit for an infinite amount of time. In such a case we are bound to see some kind of stable configuration similar to what we’d see in the game of life eventually. Now imagine we have an infinite amount of computers stretched all through space. We would not need to wait to see complex order. Since all of the cellular automaton are stretch infinitely through space and time we would inevitably see all possible configurations no matter how complex.

Complexity is an interesting phenomena. How our four dimensional universe emerged may never be answered without yielding more questions. However, the cleverness of collective humanity can provide some interesting insight into how complexity can emerge by letting simple rules sit for a long enough time.